什么是“线性”?
结论(省流)
-
线性回归:在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
- 线性关系:如果称一个数学函数L(x)为线性的,可以是指:
- 定义1:L(x)是个只拥有一个变数的一阶多项式函数,即是可以表示L(x)=kx+b的形式(其中k,b为常数)。
- 定义2:L(x)具有以下两个性质:
-
可加性:L(x+t)=L(x)+L(t)
-
一次齐次性: L(mx)=mL(x)}
-
需要注意这2种定义分别描述的是2类不同的事物。研究高等数学的数学家一般只认定义2(有例外,如高等数学线性回归理论中“线性函数”概念的定义),但初等数学和许多非数学学科的书籍会习惯把定义1当作线性关系的概念(有的没有明确给出定义,但确是如此理解和使用的)。这种术语间的细微差异如果不注意的话,就容易引起混淆。
-
线性函数:满足某些性质的数学函数。
-
线性回归是统计学范畴,是一种分析方法,线性函数是数学术语(还分初等数学和高等数学),是满足某种性质的数学函数。两个线性领域不同,含义不同,不能简单类比。
PS:需要注意的是,百度百科的解释和维基百科的解释差别较大,前两条摘自维基百科。
调查过程
这是一篇机器学习的笔记。 之所以没命名为 机器学习笔记 之类的是因为,这篇博客记录了我对“线性”的搜索和理解。
如果你看过斯坦福吴恩达的Machine Learning的前几节视频的话,你一定对线性回归,逻辑回归,线性决策边界,非线性决策边界有一定印象。
我在做编程题的时候我忽然对“线性”不理解了,然后就开始查线性的意思,结果就出现了线性回归,线性函数,线性关系,线性分类器,等一系列含有“线性”的术语,越来越迷糊了。
逻辑回归是线性分类器?
ex3.pdf中有这么一句话
However, logistic regression cannot form more complex hypotheses as it is only a linear classifier.3
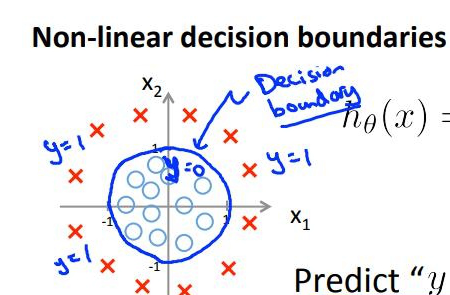
这里说逻辑回归是一个线性分类器(但是有个标注3)。 但是我记得PPT中,逻辑回归的决策边界有直线的也有非直线的,那不是说逻辑回归也可以是非线性分类器吗?怎么和这里冲突了。

查看注解3.
3You could add more features (such as polynomial features) to logistic regression, but that can be very expensive to train.
添加更多特征值作为多项式到逻辑回归中,但是会大量增加训练成本。但是这里并没有提到高阶。
查看nlp.stanford.edu 提到:
In two dimensions, a linear classifier is a line. Five examples are shown in Figure 14.8 .
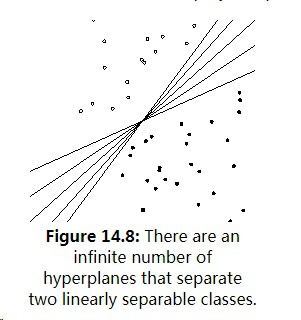
所以这里我的结论是
1, 逻辑回归是线性分类的,可以增加高阶多项式实现非线性分类,但是训练成本大大增加;
2, 线性分类器的决策边界是直线(二维的时候),否则是非线性分类。
到这里为止,线性->直线,曲线->非线性。
线性回归的拟合(Hypothesis)函数不是线性函数?
那么线性回归的拟合函数是高阶多项式的时候,这个函数是非线性函数?
我之前一直以为线性回归的多项式拟合函数是线性函数!

百度百科中的介绍感觉不是很准确,就不贴在这里了,有兴趣的自行去看一下。
之后就搜到了文章开头的维基百科的定义,好理解多了。
线性回归:在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
线性关系:如果称一个数学函数L(x)为线性的,可以是指:
- 定义1:L(x)是个只拥有一个变数的一阶多项式函数,即是可以表示L(x)=kx+b的形式(其中k,b为常数)。函数图形呈现为一条直线或线段。
- 定义2:L(x)具有以下两个性质:
- 可加性:L(x+t)=L(x)+L(t)
- 一次齐次性: L(mx)=mL(x)}
需要注意这2种定义分别描述的是2类不同的事物。研究高等数学的数学家一般只认定义2(有例外,如高等数学线性回归理论中“线性函数”概念的定义),但初等数学和许多非数学学科的书籍会习惯把定义1当作线性关系的概念(有的没有明确给出定义,但确是如此理解和使用的)。这种术语间的细微差异如果不注意的话,就容易引起混淆。
定义1的定义动机是把函数图像为直线的数量关系称作线性的关系。从这种几何意义出发,定义1本来不具有对多元函数进行推广的必要,因为形如f(x1,x2,…,xn) = k1*x1+k2*x2+…+kn*xn+b的函数(其中各个k_i和b均为常数)的图形根本不是直线,而是平面或超平面,因此也就谈不上“线”性了。
看了维基百科之后我的结论是
线性回归是统计学的一种分析方法,线性函数是描述有用某种性质的数学函数。
线性回归的拟合函数不是线性函数。
在学习线性回归最初,我们假设的拟合函数h(x)=a*x是线性函数,但是增加常数项和高阶次项以后就不再是线性函数了。
个人理解,如有错误还请指正。